Several methods are used by the Alkalinity Calculator to determine the carbonate and bicarbonate endpoints of your titration data. After these equivalence points are found, the Alkalinity Calculator then calculates the sample's alkalinity and its concentrations of hydroxide, carbonate, and bicarbonate.
To see how the program has evolved over time, please read the version history.
The inflection point method, also known as the incremental equivalence method, determines the carbonate and bicarbonate endpoints in the titration by finding the greatest change in the measured pH per unit volume of acid added. This depends on the presence of a discernable inflection point in the measured titration curve. If the alkalinity is very low, such inflection points may or may not be visible in the data.
If more than one pair of data points produces the same maximum change in pH per unit of acid added in the region of the expected endpoint, the endpoint is set at the average titrant volume of the first and last such points, and the endpoint pH at that titrant volume is interpolated. This method may be different from some other programs that you may have used in the past, but it is consistent with the latest recommendations in the USGS National Field Manual.
The carbonate endpoint will not be determined if the highest pH in the data set is less than or equal to 8.3. The search for the carbonate endpoint is restricted to the range of measured pH values less than pK2 and greater than pK1. pK1 is equal to -log10(K1), where K1 is the first acid dissociation constant of carbonic acid. pK2 is equal to -log10(K2), where K2 is the second acid dissociation constant of carbonic acid. This restricts the search to the approximate pH range between 10.3 and 6.3.
The search for the bicarbonate endpoint is restricted to the range of measured pH values less than or equal to pK1, which is about 6.3. If no titration data are available in this pH range, the analysis will be abandoned.
The fixed endpoint method determines the alkalinity and other results of the titration based on one or more user-specified endpoints. If only one endpoint is specified, the other endpoint (if necessary) is found using the inflection point method. If necessary, a linear interpolation will be used to determine the volume of titrant used at the specified endpoint pH.
If a carbonate endpoint is specified, it will be used only if the specified endpoint is within the range of the measured pH data.
The fixed endpoint method can be useful in the event that one or more of the other methods fail to detect the correct endpoint. Due to the fact that the location of the equivalence points cannot be predicted accurately in advance, however, it is inadvisable to use the fixed endpoint method to the exclusion of all other methods.
Using the theoretical equation for a carbonate titration, this method finds the carbonate and bicarbonate endpoints separately using a nonlinear least-squares fitting technique.
The carbonate endpoint is determined only if the highest pH in the data set is greater than 8.3 and at least three data points are within one pH unit of the expected endpoint. The expected endpoint is estimated with one of several methods; the default endpoint is the average of pK1 and pK2. Generally, this range is from about pH 7.3 to 9.3, but decreases when the concentration of carbonate and bicarbonate is low.
The bicarbonate endpoint will be determined only if at least three data points are within about one pH unit from the expected endpoint. The expected endpoint is estimated with one of several methods; the default range is between (pK1 - 0.6) and (pK1 - 3.1) pH units. Generally, this range is from about pH 5.8 to 3.3, but ranges higher when the concentration of bicarbonate is low.
This method finds the best fit of the theoretical carbonic acid titration curve near each endpoint by minimizing the sum of squared residuals between the measured and predicted volumes of titrant at each measured pH. Powell's conjugate direction set method, discarding the direction of largest decrease, is used to minimize this nonlinear function. Powell's method, as used in this program, was adapted to Perl from the Fortran code given in Numerical Recipes by Press et al. (1989).
The equation used to describe the theoretical carbonic acid titration curve accounts for temperature and activity effects as well as dilution of the sample by the titrant. This equation is:
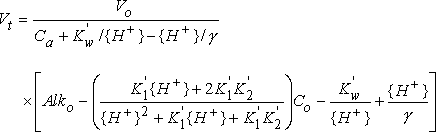
where
| Vt | is the volume of acid titrant added |
| Vo | is the initial volume of the sample |
| Ca | is the normality of the acid titrant |
| Kw' | is the acid dissociation constant for water |
| {H+} | is the hydrogen ion activity |
| is the activity coefficient for H+ | |
| Alko | is the alkalinity of the sample |
| K1' | is the first acid dissociation constant for H2CO3 |
| K2' | is the second acid dissociation constant for H2CO3 |
| Co | is the sum of the carbonic acid, bicarbonate, and carbonate concentrations |
The only unknown variables in the above equation are Alko and Co. Powell's method is used to find the best-fit values for these variables. Once these values are known, the theoretical endpoints and the carbonate and bicarbonate concentrations can be calculated directly.
Both temperature and activity corrections are applied to the acid dissociation constants for water and carbonic acid. The mixed constants used by this method are defined as:
![]()
![]()
![]()
where concentrations are indicated by square brackets
[ ], activities are denoted by braces { }, and the ![]() symbols are the activity coefficients for
the species subscripted. For more information on the chemistry of carbonic
acid in water, read Aquatic Chemistry Concepts by Pankow (1991).
symbols are the activity coefficients for
the species subscripted. For more information on the chemistry of carbonic
acid in water, read Aquatic Chemistry Concepts by Pankow (1991).
Activity corrections are based on the extended Debye-Hückel relation between activity coefficients and ionic strength. Ionic strength (I) is estimated from specific conductance (SC) as:
I = 0.000025 * 0.59 * SC
This equation is based on a relation between ionic strength and total dissolved solids, taken from Sawyer and McCarty (1967), which accounts for the first constant (0.000025), and an empirical relation between total dissolved solids and specific conductance, taken from Hem (1992), which accounts for the second constant (0.59).
The relations used to calculate the effects of temperature on the activity coefficients were taken from equations used in the water-quality model CE-QUAL-W2, version 3.1 (Cole and Wells, 2002). The acid dissociation constants are calculated as a function of temperature according to equations given by Stumm & Morgan's Aquatic Chemistry, 3rd edition (1996):
![]()
where the coefficients of the equation are:
| Coefficient | Kw | K1 | K2 |
|---|---|---|---|
| a1 | -283.9710 | -356.3094 | -107.8871 |
| a2 | -0.05069842 | -0.06091964 | -0.03252849 |
| a3 | 13323.00 | 21834.37 | 5151.79 |
| a4 | 102.24447 | 126.8339 | 38.92561 |
| a5 | -1119669 | -1684915 | -563713.9 |
and T is the absolute water temperature in degrees Kelvin. Temperature in Kelvin is obtained by adding 273.15 to the temperature in degrees Celsius.
This method is the same as the theoretical carbonate titration curve method 1, except that the fitting technique uses data from the entire titration curve rather than just from the regions near the expected endpoints.
The carbonate and bicarbonate endpoints determined by this method are guaranteed to be consistent with one another and with the chemistry of carbonic acid. By contrast, when the endpoints are fitted independently, as in the best fit method 1 above, the calculated values may not be consistent with each other. After all, method 1 above will determine two sets of values for Alko and Co if two separate endpoints are determined. This method avoids such an inconsistency.
If the sample should have a significant amount of non-carbonate alkalinity, however, the fitted titration curve may be poor. In other words, the chemistry of carbonic acid alone may not be able to account for the shape of the measured titration curve. Indications of a poor fit include systematic (non-random) deviations above or below the measured data, clear errors in the predicted endpoints, or a starting point far from the measured starting point of the titration. The amount of non-carbonate alkalinity can be estimated, but such estimates are susceptible to large errors; therefore, an estimate of the non-carbonate alkalinity is not made by this program.
This method is included specifically to give the user an indication of whether the chemistry of carbonic acid alone can account for the shape of the entire titration curve. If the fit is poor, it is unlikely that the calculated endpoints will be of much use. A poor fit does indicate, however, that the carbonate and bicarbonate concentrations calculated by the other methods actually are accounting for more than just carbonate and bicarbonate. An excellent fit with this method is evidence that the titration curve is dominated by the carbonic acid species; the calculated carbonate and bicarbonate concentrations will be fairly accurate in that case.
Gran titration analysis can be used to determine the location of the carbonate and bicarbonate endpoints (as well as other parameters such as K1', K2', and Ca) using data that are somewhat removed from the endpoints of interest. Indeed, the linearizing assumptions used by Gran's method are valid only for data that are some distance away from the endpoints (Gran, 1950 and 1952). Gran's method does not rely on the presence of inflection points in the titration curve; therefore, it is particularly useful for waters with low alkalinity.
Gran's method also can be used to determine the "hydroxide" endpoint, which often does not produce a visible inflection point in the titration curve. This is the only method used by the Alkalinity Calculator that attempts to find the hydroxide endpoint, although all of these methods can compensate for the titration of hydroxide when calculating the concentrations of carbonate and bicarbonate (if the advanced speciation method is used). The titration of hydroxide is only important in water samples with very high pH, say greater than pH 9.2.
Gran's method can be used to quantify negative values of alkalinity in solutions with an initial pH lower than the bicarbonate equivalence point. It is the only method available in the Alkalinity Calculator that can do so.
In order for Gran's method to work well, it is best to carry out acidimetric titrations to pH values well below the final endpoint. In other words, it works best for environmental samples if you provide data down to pH 3.5 or lower. In addition, because Gran's method uses data that are somewhat removed from the endpoints, it is best not to skip over any part of the titration.
Using the known chemistry of carbonic acid and some simplifying assumptions, Gran's method linearizes several functions that describe parts of the titration curve. For a derivation, read Aquatic Chemistry by Stumm and Morgan (1981) or go back to the original papers by Gunnar Gran (1950, 1952). The Gran functions are as follows:
![]()
![]()
![]()
![]()
![]()
![]()
where
| Vs | is the titrant volume at the bicarbonate endpoint |
| Vw | is the titrant volume at the carbonate endpoint |
| Vx | is the titrant volume at the hydroxide endpoint |
and the other variables are defined as above. For these functions, it is useful to know that:
![]()
Note that F2 and F3, as well as F4 and F5, are simple algebraic rearrangements of each other. Note also that functions F5 and F6 are rarely used, as the pH of the sample would have to be rather high to invoke these functions.
The Gran plot is obtained by plotting each of the Gran functions against titrant volume and fitting a line through each function's data points in a particular pH region.
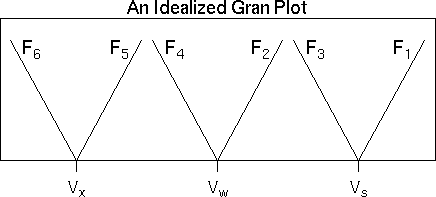
Function F1 is valid for the pH range just beyond the bicarbonate endpoint. Functions F2 and F3 are valid somewhere in the pH range between the carbonate and bicarbonate endpoints. Functions F4 and F5 are valid for pH values between the carbonate and hydroxide endpoints. Finally, function F6 is valid for pH values higher than the hydroxide endpoint.
This program does its best to fit a line through the points in each of these functions' linear ranges. This is not a trivial task. If the fitted lines don't work well for your particular data set, you may want to do your own Gran titration analysis. The potential error in the results increases when the lines derived from the Gran functions are based on only a few points. Beware of results that are derived from only two points!
Once the fitted lines are obtained, the various endpoints can be found by determining the titrant volume where each function crosses the Y axis.
You may note that in order to calculate F2, one needs to have a value for Vs, which is obtained from the solution of F1. Similarly, the value of Vw from an analysis of F2 is necessary to plot and analyze F3. Function F4 requires both Vs and Vw, from the results of F2 and either F1 or F3. Function F5 requires a value for Vw from the results of either F2 or F4.
If F1 cannot be solved, then this method estimates F3 using a zero value for Vw. The value for Vs obtained from F3, then, is used in calculating F2. If a value of Vw is obtained from F2, then F3 (and then F2) is re-evaluated. Function F4 is only calculated if the results from F2 and from either F1 or F3 are available. Functions F5 and F6 are attempted only if a value for Vw could be found from F2. Complicated? Well, yes. But, it seems to work most of the time.
The concentrations of carbonate and bicarbonate in the sample are calculated using either a simple mass-balance speciation method (deprecated-- no longer used) or an advanced speciation method. Either way, the calculation of the sample alkalinity is a straightforward accounting of the acid used to neutralize the sample, and the hydroxide concentration is easily calculated from the sample's initial pH. The equation for calculating alkalinity is documented in section 6.6.5.A of the USGS National Field Manual.
| Constituent | Units | Equation |
|---|---|---|
| Alko | meq/L | 1000 (B) Ca (CF) / Vo |
| mg/L as CaCO3 | 50044 (B) Ca (CF) / Vo | |
| OH- | meq/L | 1000 Kw' 10pH |
| mg/L as OH- | 17007 Kw' 10pH |
where
| Alko | is the alkalinity of the sample |
| B | is the volume of titrant needed to reach the HCO3- equivalence point |
| Ca | is the normality of the acid titrant (eq/L) |
| CF | is the acid correction factor |
| Vo | is the initial volume of the sample (mL) |
| Kw' | is the acid dissociation constant for water, and |
| pH | is the initial pH of the sample |
B must be in units of milliliters. If the titration is performed with a Hach digital titrator, digital counts may be converted to milliliters by dividing the number of counts by 800.
The simple mass-balance method for determining concentrations of carbonate and bicarbonate in a titrated water sample is an old approach that is no longer used by USGS or the Alkalinity Calculator (starting with version 2.22 // 22-Sep-2012); see USGS Office of Water Quality Technical Memorandum 2012.05 for more information. For purposes of documentation only, the method is described here. The simple mass-balance speciation method works relatively well only for samples with a pH less than 9.2. In such cases, most of the alkalinity can be attributed to bicarbonate. The higher the sample pH, the greater the potential error.
This method assumes that all of the acid added above the carbonate equivalence point neutralizes only carbonate, and that all of the acid added between the carbonate and bicarbonate equivalence points neutralizes only bicarbonate. Hydroxide is not considered. The concentration of hydroxide may be calculated independently from the sample pH, but should not be considered, as any alkalinity due to hydroxide is lumped by this method into the estimated concentration of carbonate. The chemistry of carbonic acid is ignored completely.
Despite these limitations and assumptions, this simple method works relatively well for samples with a pH less than or equal to 9.2. Testing with a theoretical titration indicates that if this method is used for samples with pH less than 9.2, errors due solely to the speciation method should be restricted to less than 10 percent, or less than 1 mg/L.
The speciation equations used by the simple mass-balance speciation method are:
| Constituent | Units | Equation |
|---|---|---|
| HCO3- | meq/L | 1000 (B - 2A) Ca (CF) / Vo |
| mg/L as HCO3- | 61017 (B - 2A) Ca (CF) / Vo | |
| CO32- | meq/L | 2000 (A) Ca (CF) / Vo |
| mg/L as CO32- | 60009 (A) Ca (CF) / Vo |
where
| A | is the volume of titrant needed to reach the CO32- equivalence point |
| B | is the volume of titrant needed to reach the HCO3- equivalence point |
| Ca | is the normality of the acid titrant |
| CF | is the acid correction factor, and |
| Vo | is the initial volume of the sample |
Both A and B must be in milliliters. If the titration is performed with a Hach digital titrator, digital counts may be converted to milliliters by dividing the number of counts by 800.
If the value of B is determined to be less than zero using Gran's method, the bicarbonate concentration is set to zero. If the initial sample pH is greater than 8.3 and A is not determined, then this method fails and the concentrations of carbonate and bicarbonate are not calculated. Again, this method is deprecated; see USGS Office of Water Quality Technical Memorandum 2012.05 for more information and use the advanced speciation method instead.
In this method, the concentrations of hydroxide, carbonate, and bicarbonate are calculated from the sample pH and alkalinity, according to well-known theoretical relations. Underlying these relations is the assumption that the chemistry of carbonic acid accounts for all of the significant alkalinity in the sample. If any other species with acid/base properties (such as borate, silicate, ammonia, etc.) are present in significant concentrations, then the calculated concentrations of carbonate and bicarbonate will be in error.
The equations for hydroxide, carbonate, and bicarbonate are as follows:
![]()
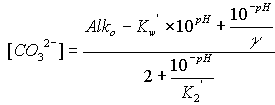
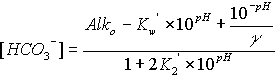
where the symbols are used as defined above, Alko is in units of equivalents per liter, and the concentrations of hydroxide, carbonate, and bicarbonate are in moles per liter. To convert to milliequivalents per liter (meq/L), multiply moles per liter by 1000 for hydroxide or bicarbonate, and by 2000 for carbonate. To convert moles per liter to milligrams per liter (mg/L), multiply the bicarbonate result by 61,017.1, the carbonate result by 60,009.2, and the hydroxide result by 17,007.3. The concentrations of hydroxide, carbonate, and bicarbonate are constrained to be non-negative.
Note that these equations are different from those that the USGS had traditionally used for the calculation of carbonate and bicarbonate concentrations. Those older equations (see the simple mass-balance method above) did not account for the possible titration of significant amounts of hydroxide, and they did not take into account the equilibrium chemistry of the carbonate species. These oversights made the calculations simpler, and the old equations worked well for many samples, but those equations should not be used for any sample with a pH greater than 9.2. The equations used in this advanced speciation method, however, are valid for any sample pH, include the effects of hydroxide, and consider the equilibrium chemistry of the carbonate species. For these reasons, the advanced speciation method is the only speciation method offered in the Alkalinity Calculator since version 2.22 // 22-Sep-2012.
Cole, T.M., and Wells, S.A., 2002, CE-QUAL-W2: A two-dimensional, laterally averaged, hydrodynamic and water quality model, version 3.1: U.S. Army Corps of Engineers Instruction Report EL-02-1 [variously paged].
Gran, G., 1950, Determination of the equivalence point in potentiometric titrations, Acta Chemica Scandinavica, 4, 559-577.
Gran, G., 1952, Determination of the equivalence point in potentiometric titrations-- Part II, The Analyst, 77, 661-671.
Hem, J.D., 1985, Study and interpretation of chemical characteristics of natural water: U.S. Geological Survey Water-Supply Paper 2254, 263 p. (Also available at http://pubs.usgs.gov/wsp/wsp2254/.)
Pankow, J.F., 1991, Aquatic chemistry concepts: Chelsea, Michigan, Lewis Publishers, 673 p.
Press, W.H., Flannery, B.P., Teukolsky, S.A., and Vetterling, W.T., 1989, Numerical recipes -- The art of scientific computing (Fortran version): New York, Cambridge University Press, 702 p.
Rounds, S.A., 2012, Alkalinity and acid neutralizing capacity (version 4.0), in National field manual for the collection of water-quality data, Wilde, F.D. and Radtke, D.B., eds., U.S. Geological Survey Techniques of Water-Resources Investigations, Book 9, Chapter A6, Section 6.6, 45 p. (Also available at http://water.usgs.gov/owq/FieldManual/Chapter6/section6.6/.)
Sawyer, C.N. and McCarty, P.L., 1967, Chemistry for sanitary engineers, 2nd ed.: McGraw-Hill, St. Louis, MO
Stumm, W. and Morgan, J.J., 1981, Aquatic chemistry, 2nd ed.: New York, John Wiley & Sons, 780 p.
Stumm, W. and Morgan, J.J., 1996, Aquatic chemistry: Chemical equilibria and rates in natural waters, 3rd ed.: New York, John Wiley & Sons, 1022 p.
U.S. Geological Survey, 2012, Replacement of the simple speciation method for computation of carbonate and bicarbonate concentrations from alkalinity titrations: Office of Water Quality Technical Memorandum 2012.05, accessed September 16, 2012, at http://water.usgs.gov/admin/memo/QW/qw12.05.pdf.
Home |
Version History |
Speciation Criteria |
Reporting Tips
Acid Lot Info |
FAQ |
Download